Absolute Zero Reasoner

Abstract & Motivation

Current reasoning models trained with Reinforcement Learning with Verifiable Rewards (RLVR) often rely on manually curated datasets, raising scalability concerns and potentially limiting future AI growth beyond human-defined tasks. To address this, we propose the Absolute Zero paradigm, where a single model autonomously proposes tasks optimized for its own learning and improves by solving them through self-play, entirely eliminating the need for external data. This approach uses feedback from a verifiable environment, ensuring grounded learning and preventing reward hacking.

Our implementation, the Absolute Zero Reasoner (AZR), leverages this paradigm for code-based reasoning. AZR uses a code executor to validate self-generated tasks (covering deduction, abduction, and induction) and verify solutions, providing reliable rewards for training. Despite using zero human-curated data, AZR achieves state-of-the-art results on diverse coding and math reasoning benchmarks, even outperforming models trained on large in-domain datasets. This demonstrates the potential for sophisticated reasoning skills to emerge purely through self-play without domain-specific supervision.

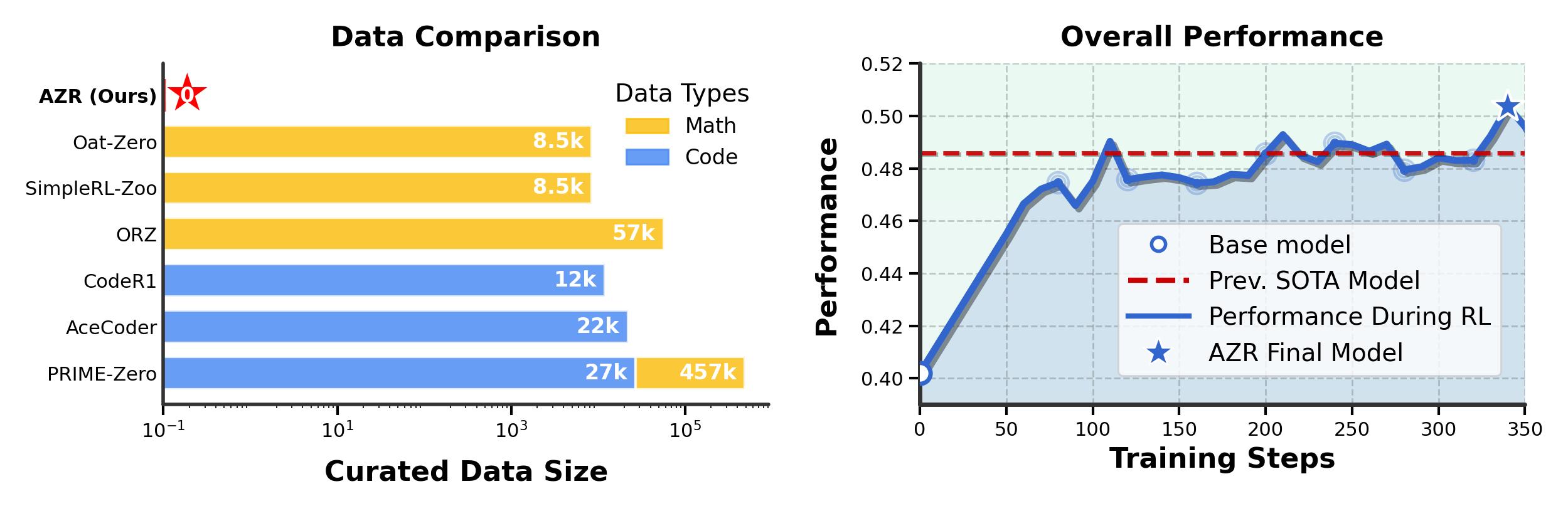
AZR Proposed Programs

All AZR proposed code samples are first embedded with jina-embeddings-v2-base-code then projected to 2D using UMAP.

Try different models

Hover over dots to explore programs. Click to lock selection.

Python Code

Input

Output

Task Information

Training Step

Spinning Hexagon Vibe Check

Prompt: Write a script that shows 10 balls bouncing inside a spinning hexagon. The balls should be affected by gravity and friction, and must bounce off the rotating walls realistically

AZR-Coder-14b (Ours)

Code


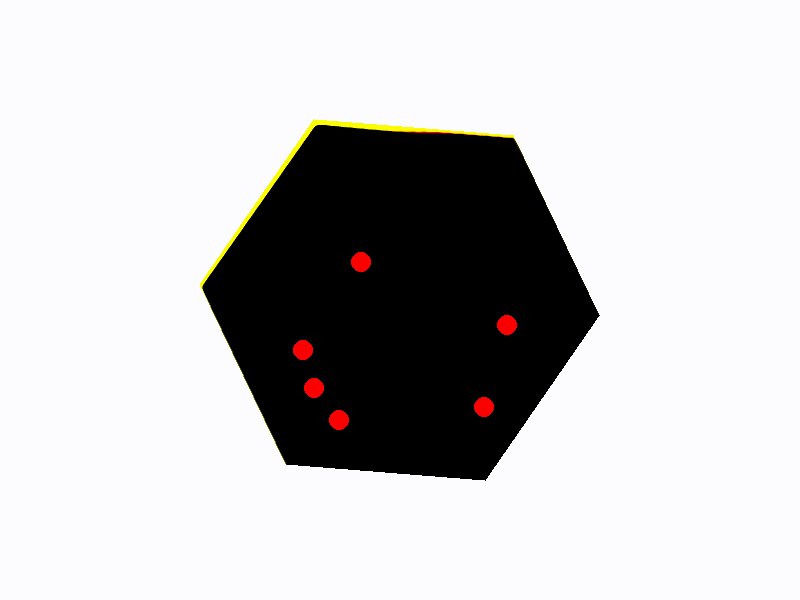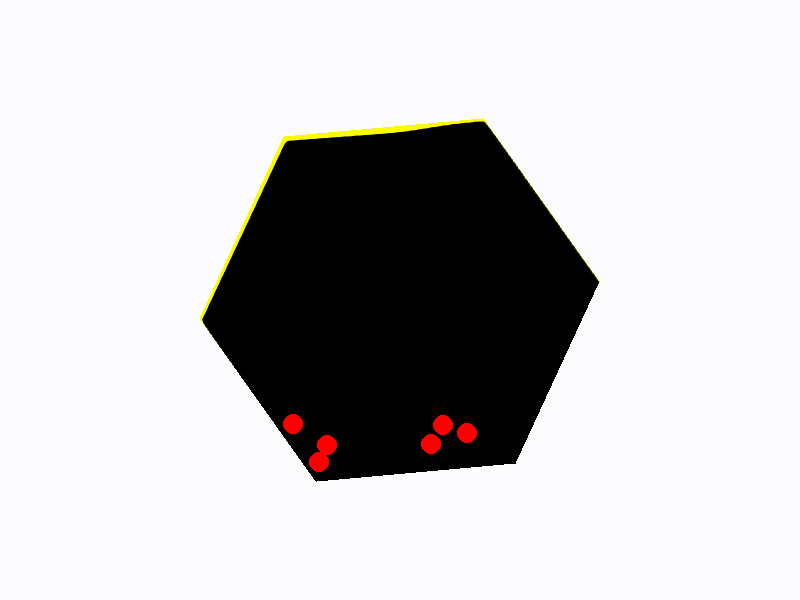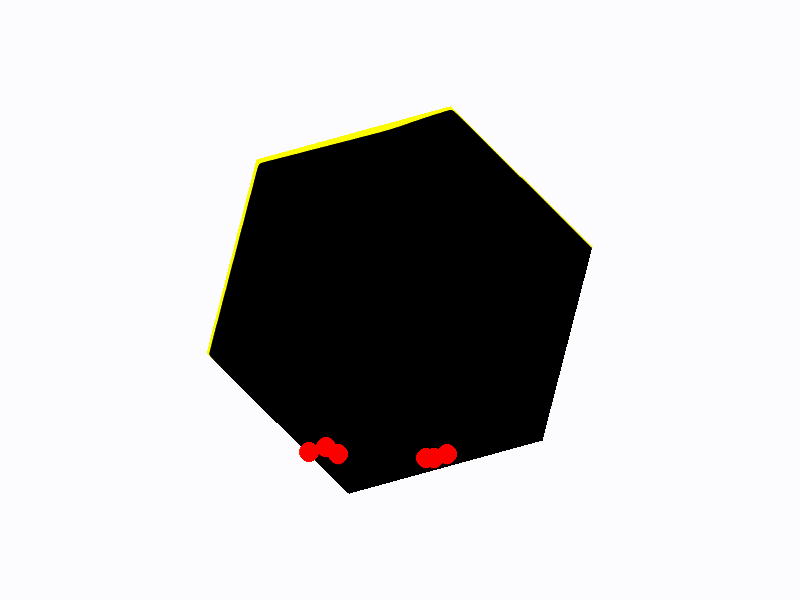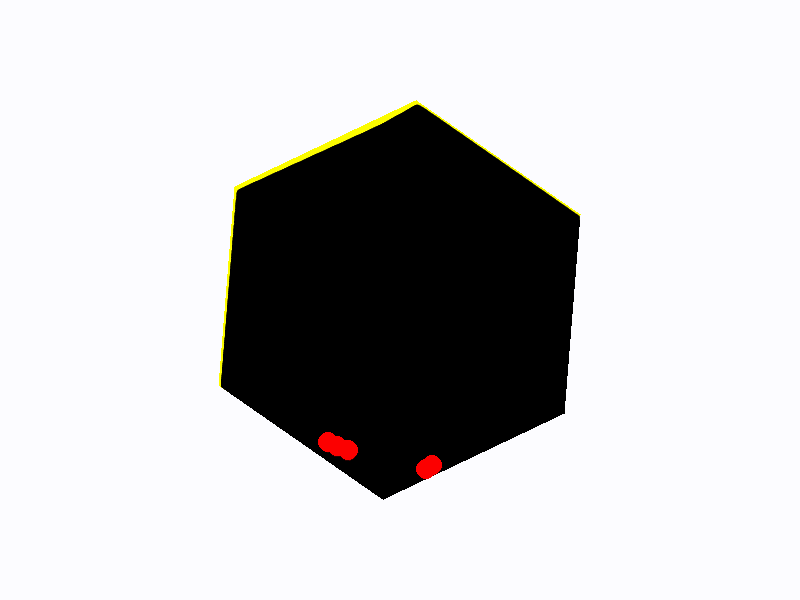
import pygame
import math
import random

# Initialize Pygame
pygame.init()

# Set up the display
width, height = 800, 600
screen = pygame.display.set_mode((width, height))
pygame.display.set_caption("Bouncing Balls in a Spinning Hexagon")

# Define colors
WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
RED = (255, 0, 0)

# Define constants
FPS = 60
GRAVITY = 0.1
FRICTION = 0.99
BALL_RADIUS = 10
NUM_BALLS = 10

# Define the hexagon
hexagon_center = (width // 2, height // 2)
hexagon_radius = 200
hexagon_vertices = [
    (hexagon_center[0] + hexagon_radius * math.cos(2 * math.pi * i / 6),
        hexagon_center[1] + hexagon_radius * math.sin(2 * math.pi * i / 6))
    for i in range(6)
]

# Define the balls
balls = []
for _ in range(NUM_BALLS):
    x = random.randint(BALL_RADIUS, width - BALL_RADIUS)
    y = random.randint(BALL_RADIUS, height - BALL_RADIUS)
    vx = random.uniform(-5, 5)
    vy = random.uniform(-5, 5)
    balls.append((x, y, vx, vy, RED))

# Game loop
running = True
clock = pygame.time.Clock()
angle = 0
while running:
    # Handle events
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    # Clear the screen
    screen.fill(WHITE)

    # Rotate the hexagon
    angle += 0.01
    rotated_vertices = [
        (hexagon_center[0] + (v[0] - hexagon_center[0]) * math.cos(angle) - (v[1] - hexagon_center[1]) * math.sin(angle),
            hexagon_center[1] + (v[0] - hexagon_center[0]) * math.sin(angle) + (v[1] - hexagon_center[1]) * math.cos(angle))
        for v in hexagon_vertices
    ]

    # Draw the hexagon
    pygame.draw.polygon(screen, BLACK, rotated_vertices)

    # Update the positions and velocities of the balls
    for i, (x, y, vx, vy, color) in enumerate(balls):
        # Apply gravity
        vy += GRAVITY

        # Apply friction
        vx *= FRICTION
        vy *= FRICTION

        # Update position
        x += vx
        y += vy

        # Check for collisions with the hexagon walls
        for j in range(6):
            v1 = rotated_vertices[j]
            v2 = rotated_vertices[(j + 1) % 6]
            dx = v2[0] - v1[0]
            dy = v2[1] - v1[1]
            dist = math.sqrt(dx**2 + dy**2)
            nx = dy / dist
            ny = -dx / dist
            px = x - v1[0]
            py = y - v1[1]
            proj = px * nx + py * ny
            if 0 <= proj <= dist:
                if px * ny - py * nx <= BALL_RADIUS:
                    overlap = BALL_RADIUS - (px * nx + py * ny)
                    x -= overlap * nx
                    y -= overlap * ny
                    vx = -vx * 0.9
                    vy = -vy * 0.9

        # Check for collisions with the screen edges
        if x - BALL_RADIUS < 0 or x + BALL_RADIUS > width:
            vx = -vx
        if y - BALL_RADIUS < 0 or y + BALL_RADIUS > height:
            vy = -vy

        # Update the ball's position and velocity
        balls[i] = (x, y, vx, vy, color)

        # Draw the ball
        pygame.draw.circle(screen, color, (int(x), int(y)), BALL_RADIUS)

    # Update the display
    pygame.display.flip()
    clock.tick(FPS)

# Quit Pygame
pygame.quit()

Config


{
    "parameters": {
        "temperature": 0.6,
        "top_p": 0.8
    },
    "generation_config": {
        "do_sample": true
    }
}

GPT-4o-mini

Code


        
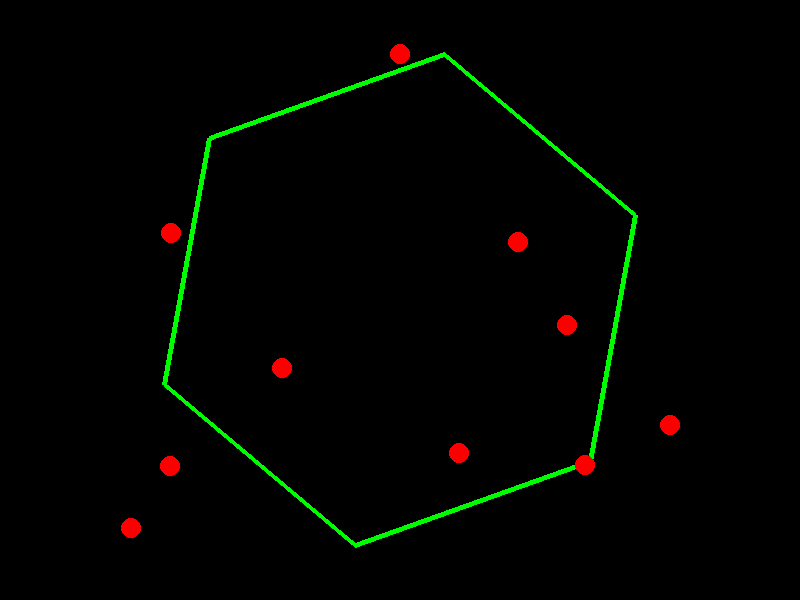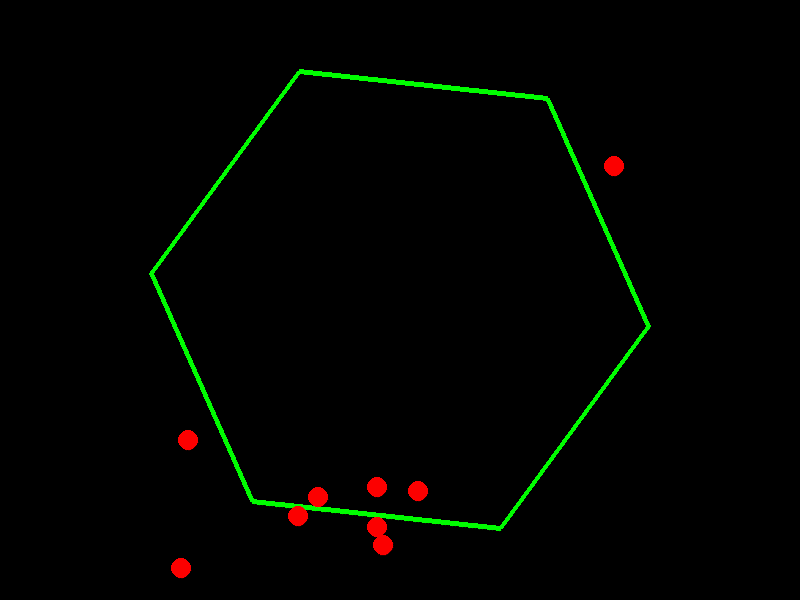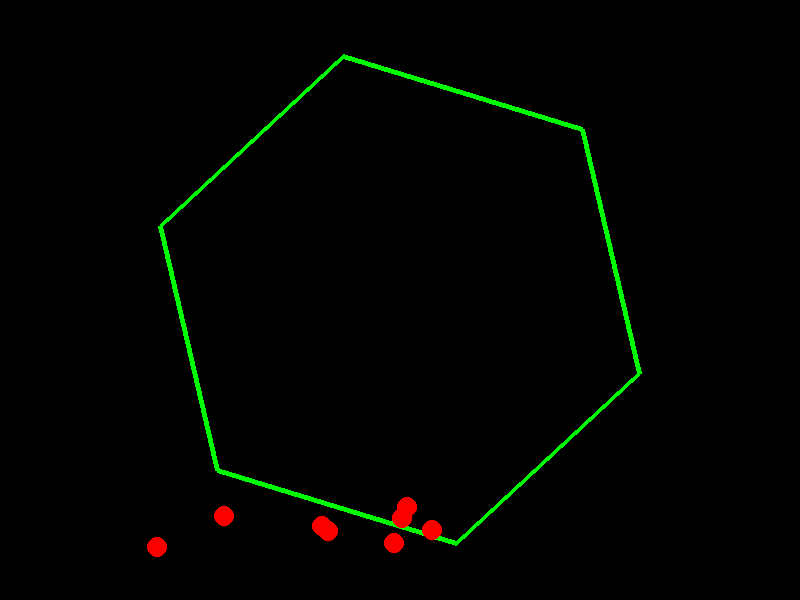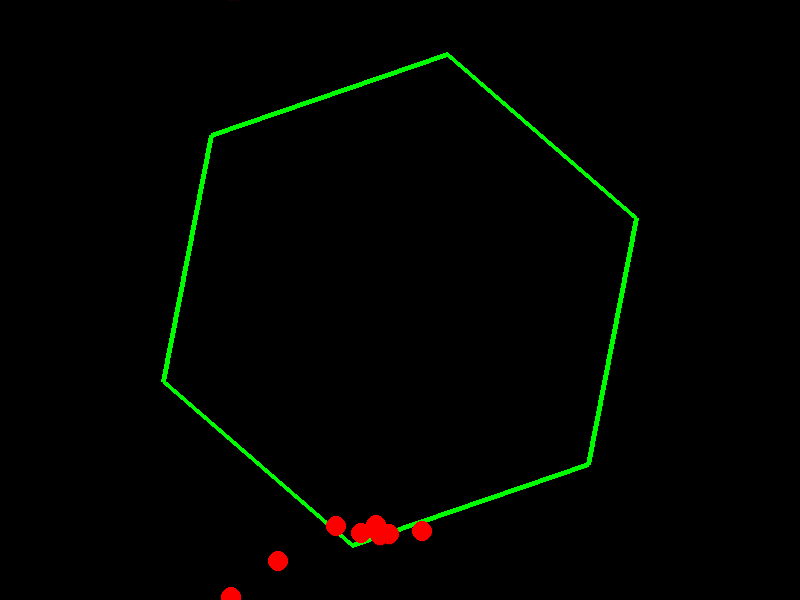
import pygame
import random
import math

# Initialize Pygame
pygame.init()

# Screen settings
WIDTH, HEIGHT = 800, 600
screen = pygame.display.set_mode((WIDTH, HEIGHT))
pygame.display.set_caption('Bouncing Balls in Spinning Hexagon')

# Colors
WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
BALL_COLOR = (255, 0, 0)
HEX_COLOR = (0, 255, 0)

# Constants
GRAVITY = 0.1  # Gravity affecting the balls
FRICTION = 0.99  # Friction affecting the ball's speed when not bouncing
BALL_RADIUS = 10  # Radius of the balls
NUM_BALLS = 10  # Number of balls

# Hexagon settings
HEX_SIZE = 250  # Hexagon radius
HEX_CENTER = (WIDTH // 2, HEIGHT // 2)

# Ball class
class Ball:
    def __init__(self, x, y, radius):
        self.x = x
        self.y = y
        self.radius = radius
        self.vx = random.uniform(-2, 2)  # Initial x velocity
        self.vy = random.uniform(-2, 2)  # Initial y velocity

    def move(self):
        self.x += self.vx
        self.y += self.vy
        self.vy += GRAVITY  # Apply gravity

        # Apply friction
        self.vx *= FRICTION
        self.vy *= FRICTION

    def bounce(self, normal):
        # Reflect the ball's velocity based on the surface normal (for realistic bouncing)
        dot = self.vx * normal[0] + self.vy * normal[1]
        self.vx -= 2 * dot * normal[0]
        self.vy -= 2 * dot * normal[1]

# Function to draw the hexagon
def draw_hexagon(angle):
    points = []
    for i in range(6):
        x = HEX_CENTER[0] + HEX_SIZE * math.cos(math.radians(i * 60 + angle))
        y = HEX_CENTER[1] + HEX_SIZE * math.sin(math.radians(i * 60 + angle))
        points.append((x, y))
    pygame.draw.polygon(screen, HEX_COLOR, points, 5)

# Function to check if the ball is inside the hexagon
def check_collision_with_hexagon(ball):
    angle = pygame.time.get_ticks() / 10  # Time-dependent rotation angle

    # Hexagon vertices (rotated)
    hex_points = []
    for i in range(6):
        x = HEX_CENTER[0] + HEX_SIZE * math.cos(math.radians(i * 60 + angle))
        y = HEX_CENTER[1] + HEX_SIZE * math.sin(math.radians(i * 60 + angle))
        hex_points.append((x, y))

    for i in range(6):
        p1 = hex_points[i]
        p2 = hex_points[(i + 1) % 6]
        
        # Calculate the normal vector of the edge
        edge = (p2[0] - p1[0], p2[1] - p1[1])
        normal = (-edge[1], edge[0])  # Perpendicular to the edge

        # Normalize the normal
        length = math.sqrt(normal[0]**2 + normal[1]**2)
        normal = (normal[0] / length, normal[1] / length)

        # Check if the ball is outside the hexagon (distance from the center to the edge)
        ball_to_edge = (ball.x - p1[0], ball.y - p1[1])
        dist = ball_to_edge[0] * normal[0] + ball_to_edge[1] * normal[1]
        
        if dist < ball.radius:
            ball.bounce(normal)
            break

# Create a list of balls
balls = [Ball(random.randint(50, WIDTH-50), random.randint(50, HEIGHT-50), BALL_RADIUS) for _ in range(NUM_BALLS)]

# Main game loop
running = True
clock = pygame.time.Clock()

while running:
    screen.fill(BLACK)  # Clear screen
    
    # Handle events
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    # Draw the spinning hexagon
    angle = pygame.time.get_ticks() / 10  # Get a time-based rotation angle
    draw_hexagon(angle)

    # Update and draw the balls
    for ball in balls:
        ball.move()
        check_collision_with_hexagon(ball)
        
        # Draw ball
        pygame.draw.circle(screen, BALL_COLOR, (int(ball.x), int(ball.y)), ball.radius)

    # Refresh the display
    pygame.display.flip()

    # Cap the frame rate
    clock.tick(60)

# Quit Pygame
pygame.quit()

Config


{
    "query_date": "2025-05-03",
    "api_location": "https://chatgpt.com/"
}

Qwen2.5-72B-Instruct

Code


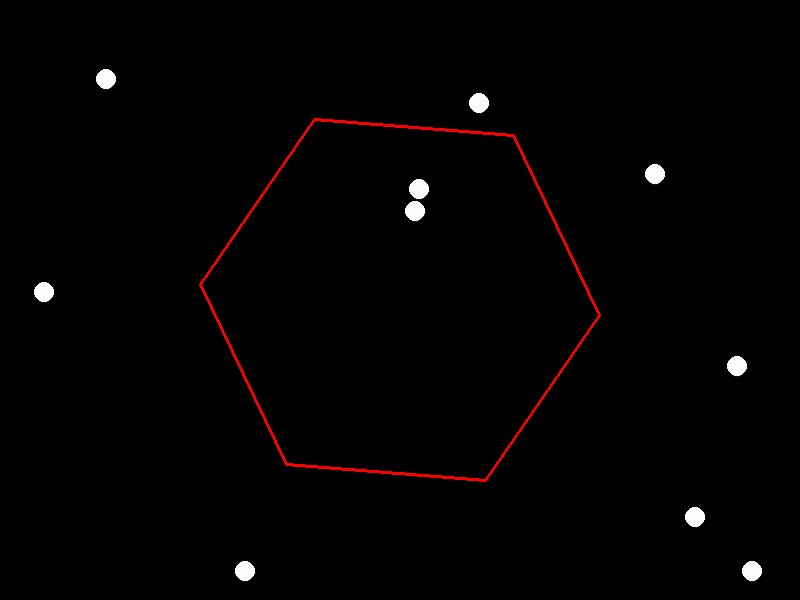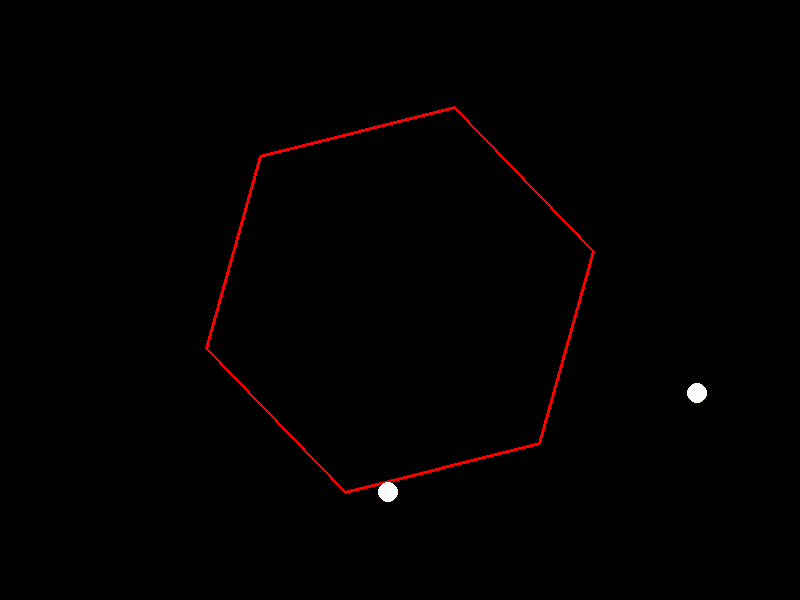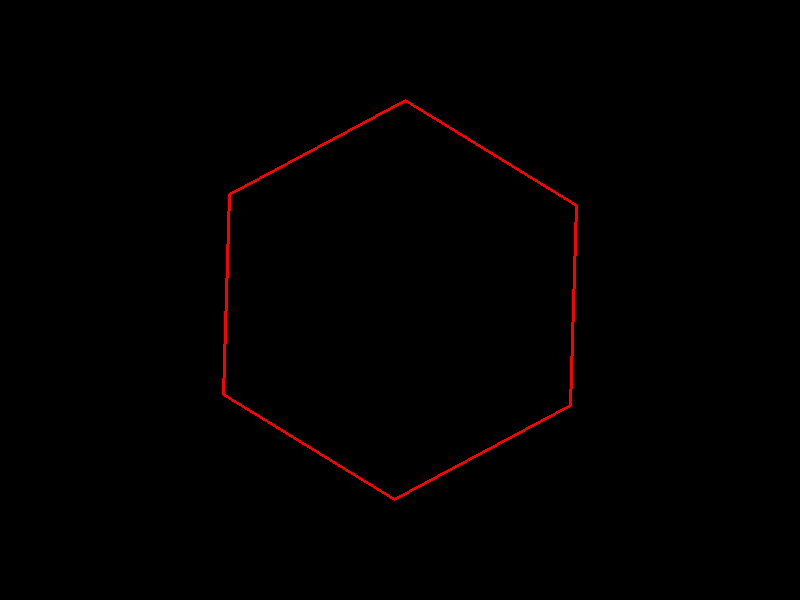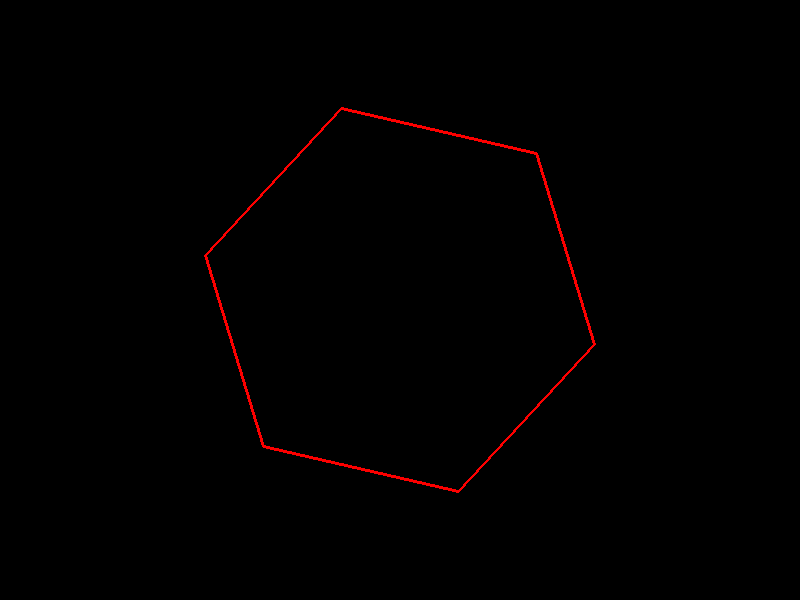
import pygame
import math
import random

# Initialize Pygame
pygame.init()

# Screen dimensions
WIDTH, HEIGHT = 800, 600
screen = pygame.display.set_mode((WIDTH, HEIGHT))
pygame.display.set_caption("Balls Bouncing in a Spinning Hexagon")

# Colors
WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
RED = (255, 0, 0)

# Hexagon properties
hexagon_center = (WIDTH // 2, HEIGHT // 2)
hexagon_radius = 200
hexagon_sides = 6
hexagon_angle = 0  # Initial angle of the hexagon
hexagon_rotation_speed = 0.01  # Rotation speed in radians per frame

# Ball properties
num_balls = 10
balls = []
ball_radius = 10
gravity = 0.5
friction = 0.99

# Function to create a ball
def create_ball():
    x = random.randint(ball_radius, WIDTH - ball_radius)
    y = random.randint(ball_radius, HEIGHT - ball_radius)
    vx = random.uniform(-3, 3)
    vy = random.uniform(-3, 3)
    return [x, y, vx, vy]

# Create balls
for _ in range(num_balls):
    balls.append(create_ball())

# Function to draw the hexagon
def draw_hexagon(angle):
    points = []
    for i in range(hexagon_sides):
        angle_i = angle + i * (2 * math.pi / hexagon_sides)
        x = hexagon_center[0] + hexagon_radius * math.cos(angle_i)
        y = hexagon_center[1] + hexagon_radius * math.sin(angle_i)
        points.append((x, y))
    pygame.draw.polygon(screen, RED, points, 3)

# Function to check collision with the hexagon
def check_collision(ball, angle):
    x, y, vx, vy = ball
    for i in range(hexagon_sides):
        angle_i = angle + i * (2 * math.pi / hexagon_sides)
        angle_next = angle + (i + 1) * (2 * math.pi / hexagon_sides)
        x1 = hexagon_center[0] + hexagon_radius * math.cos(angle_i)
        y1 = hexagon_center[1] + hexagon_radius * math.sin(angle_i)
        x2 = hexagon_center[0] + hexagon_radius * math.cos(angle_next)
        y2 = hexagon_center[1] + hexagon_radius * math.sin(angle_next)
        
        # Check collision with the line segment (x1, y1) to (x2, y2)
        dx = x2 - x1
        dy = y2 - y1
        dot = dx * (x - x1) + dy * (y - y1)
        len_sq = dx * dx + dy * dy
        param = -1
        if len_sq != 0:  # in case of a zero length line
            param = dot / len_sq
        
        if param < 0:
            nx = x1
            ny = y1
        elif param > 1:
            nx = x2
            ny = y2
        else:
            nx = x1 + param * dx
            ny = y1 + param * dy
        
        dx = x - nx
        dy = y - ny
        dist = math.sqrt(dx * dx + dy * dy)
        
        if dist < ball_radius:
            # Calculate the normal and tangent vectors
            nx = (x - nx) / dist
            ny = (y - ny) / dist
            tx = -ny
            ty = nx
            
            # Reflect the velocity
            dot = vx * nx + vy * ny
            vx = vx - 2 * dot * nx
            vy = vy - 2 * dot * ny
            
            # Move the ball away from the wall
            x += nx * (ball_radius - dist)
            y += ny * (ball_radius - dist)
            
            ball[0] = x
            ball[1] = y
            ball[2] = vx
            ball[3] = vy

# Main loop
running = True
clock = pygame.time.Clock()
while running:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    # Update ball positions and velocities
    for ball in balls:
        x, y, vx, vy = ball
        vy += gravity
        x += vx
        y += vy
        vx *= friction
        vy *= friction
        ball[0] = x
        ball[1] = y
        ball[2] = vx
        ball[3] = vy

        # Check collision with the hexagon
        check_collision(ball, hexagon_angle)

    # Update hexagon angle
    hexagon_angle += hexagon_rotation_speed

    # Draw everything
    screen.fill(BLACK)
    draw_hexagon(hexagon_angle)
    for ball in balls:
        pygame.draw.circle(screen, WHITE, (int(ball[0]), int(ball[1])), ball_radius)

    pygame.display.flip()
    clock.tick(60)

pygame.quit()

Config


{
    "api_location": "https://huggingface.co/Qwen/Qwen2.5-Coder-72B-Instruct"
}

Qwen2.5-32B-Instruct

Code


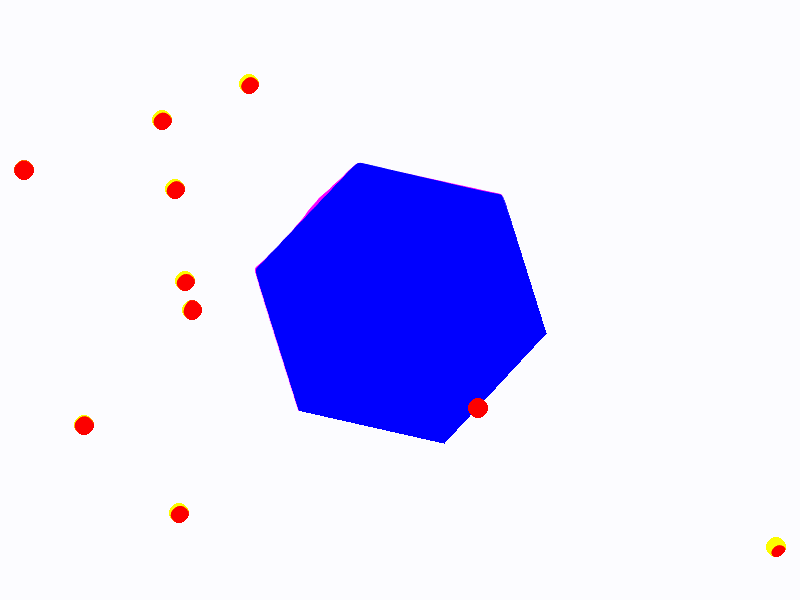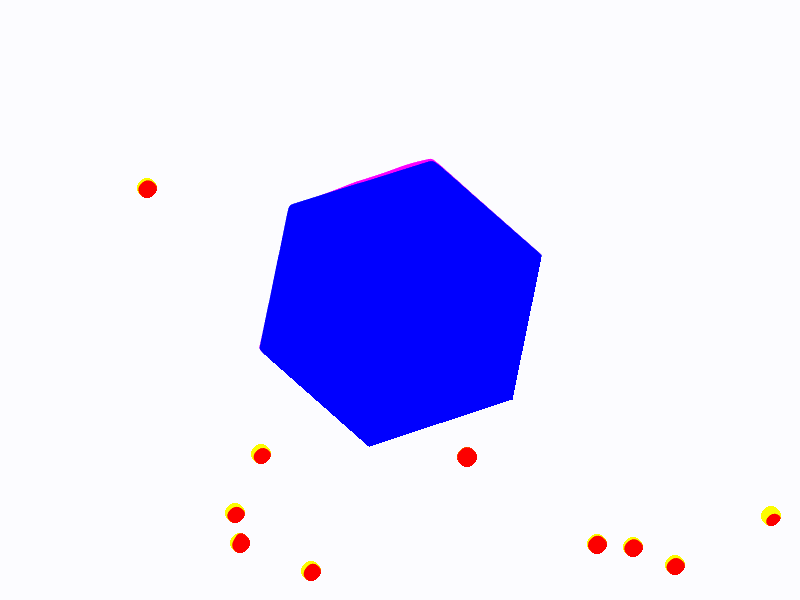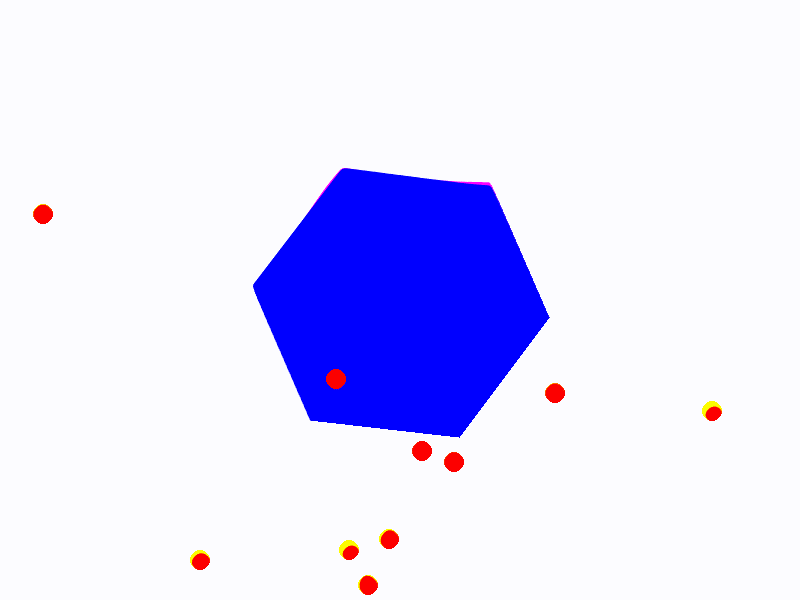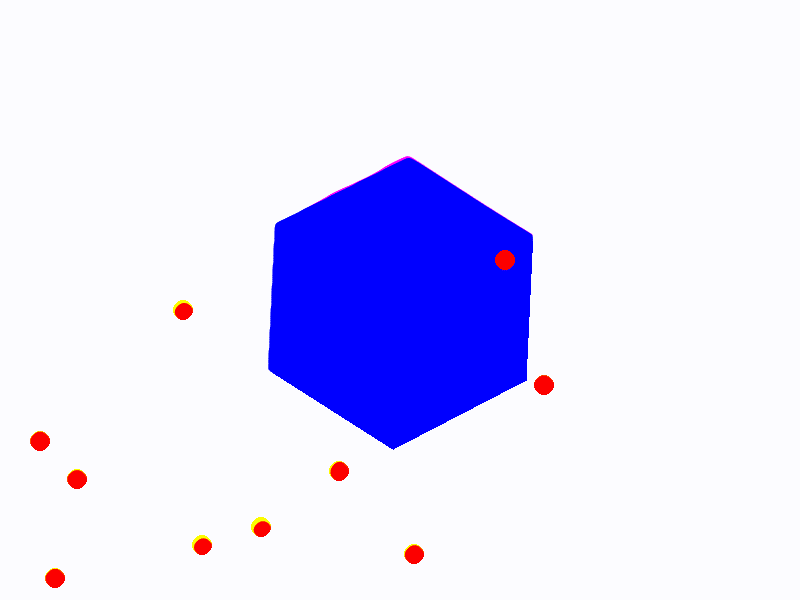
import pygame
import math
import random

# Initialize Pygame
pygame.init()

# Set up the display
screen_width, screen_height = 800, 600
win = pygame.display.set_mode((screen_width, screen_height))
pygame.display.set_caption("Bouncing Balls Inside Spinning Hexagon")

# Colors
WHITE = (255, 255, 255)
RED = (255, 0, 0)

# Constants for the simulation
FPS = 60
GRAVITY = 0.1
BALL_RADIUS = 10
FRIC_COEFFICIENT = 0.98  # To reduce velocity upon collision.
MAX_ANGLE_DEGREES = 360
DEG_TO_RAD = math.pi / 180  # Conversion factor between degrees and radians.

class Ball:
    def __init__(self):
        self.pos = pygame.Vector2(random.randint(BALL_RADIUS, screen_width-BALL_RADIUS),
                                    random.randint(BALL_RADIUS, screen_height-BALL_RADIUS))
        self.vel = pygame.Vector2(random.uniform(-3, 3), random.uniform(-3, 3))

    def update(self):
        self.vel.y += GRAVITY
        self.pos += self.vel

        # Check for collisions with borders
        if self.pos.x - BALL_RADIUS <= 0 or self.pos.x + BALL_RADIUS >= screen_width:
            self.vel.x *= -FRIC_COEFFICIENT
            if self.pos.x - BALL_RADIUS <= 0:
                self.pos.x = BALL_RADIUS
            elif self.pos.x + BALL_RADIUS >= screen_width:
                self.pos.x = screen_width - BALL_RADIUS
        if self.pos.y - BALL_RADIUS <= 0 or self.pos.y + BALL_RADIUS >= screen_height:
            self.vel.y *= -FRIC_COEFFICIENT
            if self.pos.y - BALL_RADIUS <= 0:
                self.pos.y = BALL_RADIUS
            elif self.pos.y + BALL_RADIUS >= screen_height:
                self.pos.y = screen_height - BALL_RADIUS

    def draw(self, win):
        pygame.draw.circle(win, RED, (int(self.pos.x), int(self.pos.y)), BALL_RADIUS)

def get_hexagon_points(center, radius, angle_degrees):
    """Generate points of a hexagon."""
    points = []
    for i in range(6):
        theta = (math.pi * 2) / 6 * i + angle_degrees * DEG_TO_RAD
        x = center.x + radius * math.cos(theta)
        y = center.y + radius * math.sin(theta)
        points.append(pygame.Vector2(x, y))
    return points

def check_bounce(ball, poly_points):
    """Check if the ball has hit any of the edges and bounce off appropriately."""
    p1, p2, p3, p4, p5, p6 = poly_points
    for start_point, end_point in [(p1, p2), (p2, p3), (p3, p4), (p4, p5), (p5, p6), (p6, p1)]:
        line_vec = end_point - start_point
        normal_vec = pygame.Vector2(-line_vec.y, line_vec.x).normalize()  # Normal vector to edge
        
        # Line equation parameters: Ax + By + C = 0
        A = normal_vec.y
        B = -normal_vec.x
        C = -(A * start_point.x + B * start_point.y)
        
        # Point-line-distance formula
        distance = A * ball.pos.x + B * ball.pos.y + C
        distance /= math.sqrt(A**2 + B**2)
        
        if abs(distance) < BALL_RADIUS:
            # Ball is hitting this edge.
            dist_vec = ball.pos - (start_point + end_point) / 2
            dot_product = dist_vec.dot(normal_vec)
            reflection_vec = ball.vel.reflect(normal_vec)
            
            if dot_product < 0 and reflection_vec.x * A + reflection_vec.y * B > 0:
                # Reflect and apply some slowdown using friction coefficient.
                ball.vel = reflection_vec * FRIC_COEFFICIENT

def redraw_window(win, balls, poly_points):
    win.fill(WHITE)
    pygame.draw.polygon(win, (0, 0, 255), [(p.x, p.y) for p in poly_points])
    for ball in balls:
        ball.draw(win)
    
    pygame.display.update()

def main():
    run = True
    clock = pygame.time.Clock()

    balls = [Ball() for _ in range(10)]
    hexagon_center = pygame.Vector2(screen_width // 2, screen_height // 2)
    hexagon_radius = screen_height // 4
    angle_degrees = 0

    while run:
        dt = clock.tick(FPS) / 1000  # time elapsed since last frame in seconds
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                run = False
        
        # Spin the hexagon by increasing the angle
        angle_degrees = (angle_degrees + 1 * dt * MAX_ANGLE_DEGREES) % MAX_ANGLE_DEGREES
        poly_points = get_hexagon_points(hexagon_center, hexagon_radius, angle_degrees)

        # Update each ball and check for collision with hexagon walls.
        for ball in balls:
            ball.update()
            check_bounce(ball, poly_points)

        redraw_window(win, balls, poly_points)

    pygame.quit()

if __name__ == "__main__":
    main()

Config


{
    "api_location": "https://huggingface.co/Qwen/Qwen2.5-Coder-32B-Instruct"
}

Qwen2.5-14B-Instruct

Code


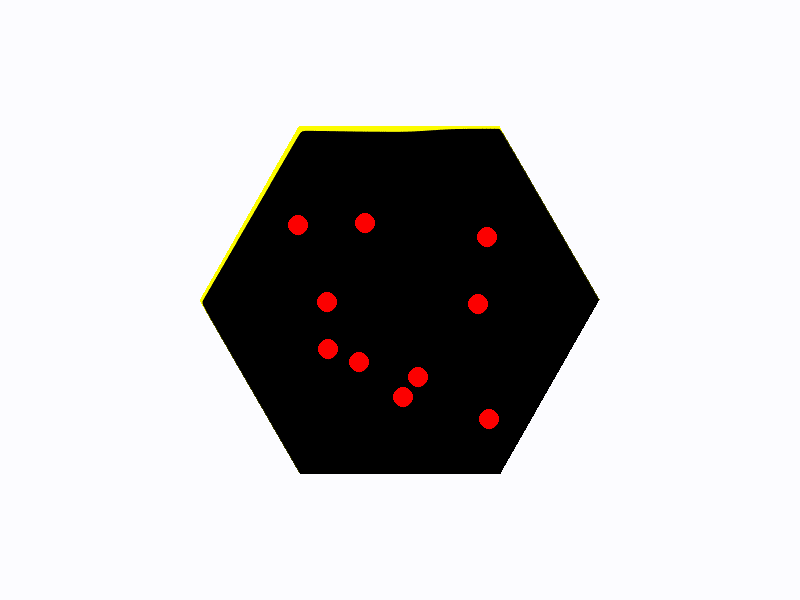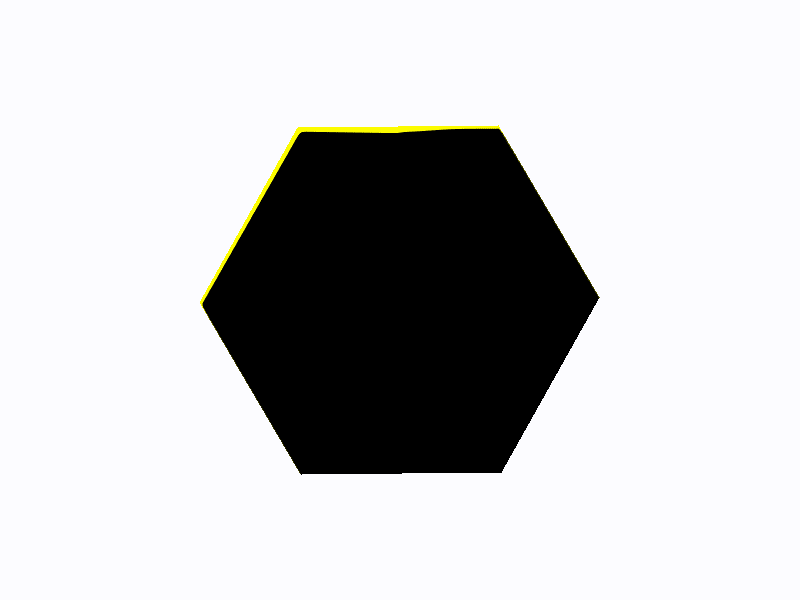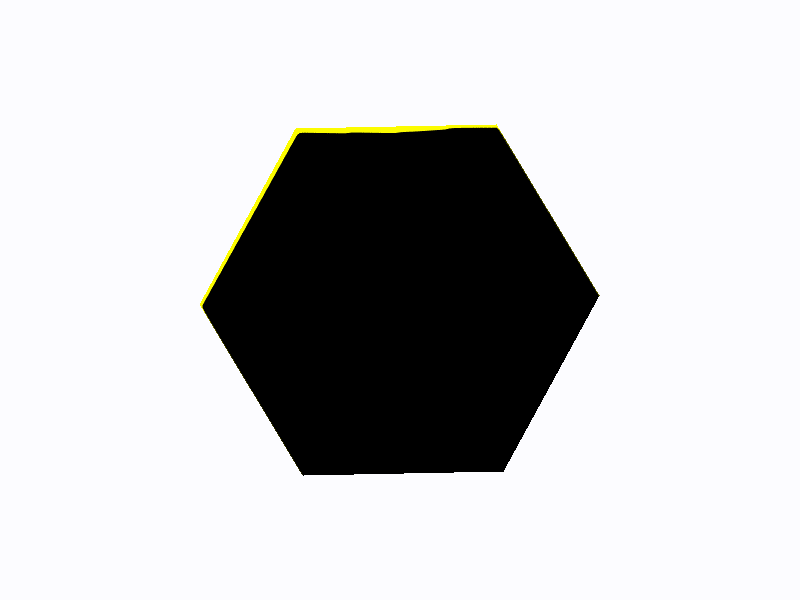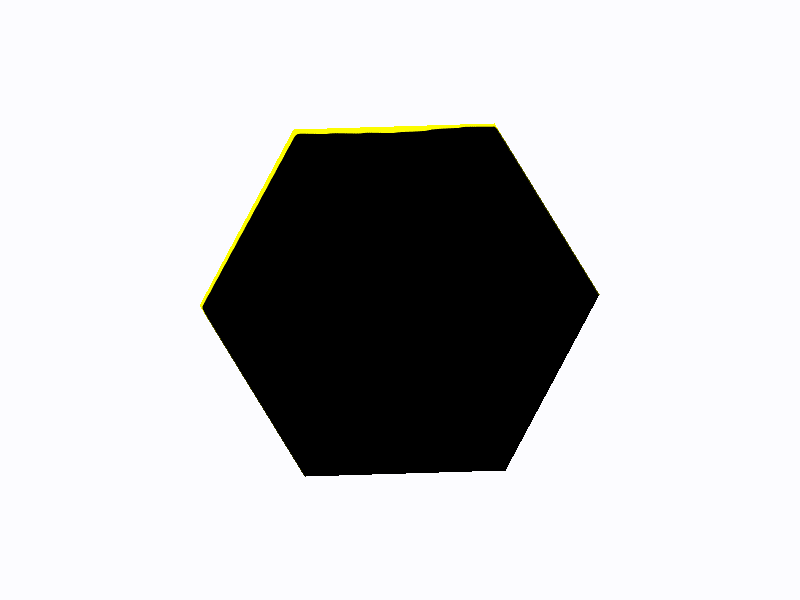
import pygame
import sys
import math
import random

# Initialize Pygame
pygame.init()

# Screen dimensions
SCREEN_WIDTH = 800
SCREEN_HEIGHT = 600
screen = pygame.display.set_mode((SCREEN_WIDTH, SCREEN_HEIGHT))
pygame.display.set_caption("Bouncing Balls in Spinning Hexagon")

# Colors
WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
RED = (255, 0, 0)

# Ball properties
BALL_RADIUS = 10
BALL_COUNT = 10
balls = []

# Hexagon properties
HEX_SIDES = 6
HEX_RADIUS = 200
HEX_CENTER = (SCREEN_WIDTH // 2, SCREEN_HEIGHT // 2)
HEX_SPIN_SPEED = 0.01

# Gravity and friction
GRAVITY = 0.5
FRICTION = 0.99

def create_balls():
    for _ in range(BALL_COUNT):
        x = SCREEN_WIDTH // 2 + (random.randint(-100, 100))
        y = SCREEN_HEIGHT // 2 + (random.randint(-100, 100))
        vx = random.uniform(-3, 3)
        vy = random.uniform(-3, 3)
        balls.append([x, y, vx, vy])

def draw_hexagon(angle):
    points = []
    for i in range(HEX_SIDES):
        angle_rad = math.radians(i * 60 - angle)
        x = HEX_CENTER[0] + HEX_RADIUS * math.cos(angle_rad)
        y = HEX_CENTER[1] + HEX_RADIUS * math.sin(angle_rad)
        points.append((int(x), int(y)))
    return points

def check_collision(ball, points):
    px, py = ball[:2]
    for i in range(len(points)):
        j = (i + 1) % len(points)
        if is_point_in_triangle(px, py, points[i], points[j], HEX_CENTER):
            return True
    return False

def is_point_in_triangle(px, py, p1, p2, p3):
    def sign(p1, p2, p3):
        return (p1[0] - p3[0]) * (p2[1] - p3[1]) - (p2[0] - p3[0]) * (p1[1] - p3[1])
    
    b1 = sign((px, py), p1, p2) < 0
    b2 = sign((px, py), p2, p3) < 0
    b3 = sign((px, py), p3, p1) < 0
    
    return ((b1 == b2) and (b2 == b3))

def update_ball(ball, points):
    x, y, vx, vy = ball
    x += vx
    y += vy
    vy += GRAVITY
    
    if check_collision(ball, points):
        # Bounce logic
        normal_vector = get_normal_vector(ball, points)
        reflect_vector(normal_vector, ball)
        
        # Apply friction
        vx *= FRICTION
        vy *= FRICTION
        
    ball[0] = x
    ball[1] = y
    ball[2] = vx
    ball[3] = vy

def get_normal_vector(ball, points):
    px, py = ball[:2]
    closest_point = min(points, key=lambda point: math.hypot(point[0] - px, point[1] - py))
    dx, dy = closest_point[0] - px, closest_point[1] - py
    length = math.sqrt(dx**2 + dy**2)
    return [dx / length, dy / length]

def reflect_vector(normal, ball):
    px, py, vx, vy = ball
    dot_product = vx * normal[0] + vy * normal[1]
    reflected_vx = vx - 2 * dot_product * normal[0]
    reflected_vy = vy - 2 * dot_product * normal[1]
    ball[2] = reflected_vx
    ball[3] = reflected_vy

def main():
    clock = pygame.time.Clock()
    angle = 0
    create_balls()
    
    while True:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                pygame.quit()
                sys.exit()
        
        screen.fill(WHITE)
        
        # Draw the hexagon
        points = draw_hexagon(angle)
        pygame.draw.polygon(screen, BLACK, points)
        
        # Update and draw balls
        for ball in balls:
            update_ball(ball, points)
            pygame.draw.circle(screen, RED, (int(ball[0]), int(ball[1])), BALL_RADIUS)
        
        angle += HEX_SPIN_SPEED
        pygame.display.flip()
        clock.tick(60)

if __name__ == "__main__":
    main()

Config


{
    "parameters": {
        "temperature": 0.6,
        "top_p": 0.8,
        "do_sample": true
    }
}

1. Absolute Zero Paradigm

Traditional approaches to training reasoning models rely heavily on human-curated data:

Supervised Fine-Tuning (SFT) requires datasets with human-written queries, rationales, and answers.
Reinforcement Learning with Verifiable Rewards (RLVR) still needs human-labeled tasks and answers, even if the model generates its own reasoning.

The Absolute Zero paradigm eliminates this dependency on human data. The model simultaneously proposes tasks, solves them, and learns from both stages through self-play. As shown in Figure 1, the agent autonomously creates tasks optimized for learnability and learns to solve them using a unified model.

The agent π acts in two roles: as a proposer π^propose that generates tasks τ, and as a solver π^solve that produces answers y. The environment e validates proposed tasks into (x, y★) pairs and provides both learnability rewards r^propose and solution rewards r^solve. This enables continuous self-improvement without any human-curated data.

2. Absolute Zero Reasoner

The Absolute Zero Reasoner (AZR) is our first implementation of the Absolute Zero Paradigm. AZR uses a unified language model that serves dual roles while learning through code-based reasoning challenges. The model works through a continuous self-improvement loop without requiring any human-curated data.

2.1. Propose and Solve Roles

The Absolute Zero Reasoner employs a unified model that acts in two complementary roles:

Proposer Role: Generates tasks with high learning potential - neither too easy nor impossible for the current solver. The model is rewarded for creating challenges that provide meaningful learning opportunities.
Solver Role: Attempts to solve the proposed problems, receiving binary rewards based on the correctness of solutions, verified through Python execution.

For the proposer, we design a specialized reward function based on Monte Carlo rollouts that encourages the generation of tasks with optimal difficulty - problems where the solver sometimes succeeds and sometimes fails. This creates the richest learning signal for continuous improvement.

2.2. Reasoning Modes

As shown in Figure 3, the Absolute Zero Reasoner operates across three fundamental reasoning modes, each focusing on different aspects of a triplet (program, input, output):

Deduction: Predicting the output given a program and input, capturing step-by-step logical reasoning. This tests the model's ability to trace program execution.
Abduction: Inferring a plausible input given a program and its output, resembling trial-and-error or search processes. This tests the model's ability to work backward from results.
Induction: Synthesizing a program from input-output examples, requiring generalization from partial information. This tests the model's ability to discover underlying patterns.

The model begins with minimal seed examples (as simple as an identity function) and bootstraps its way to increasingly complex reasoning capabilities through continual self-play and verification.

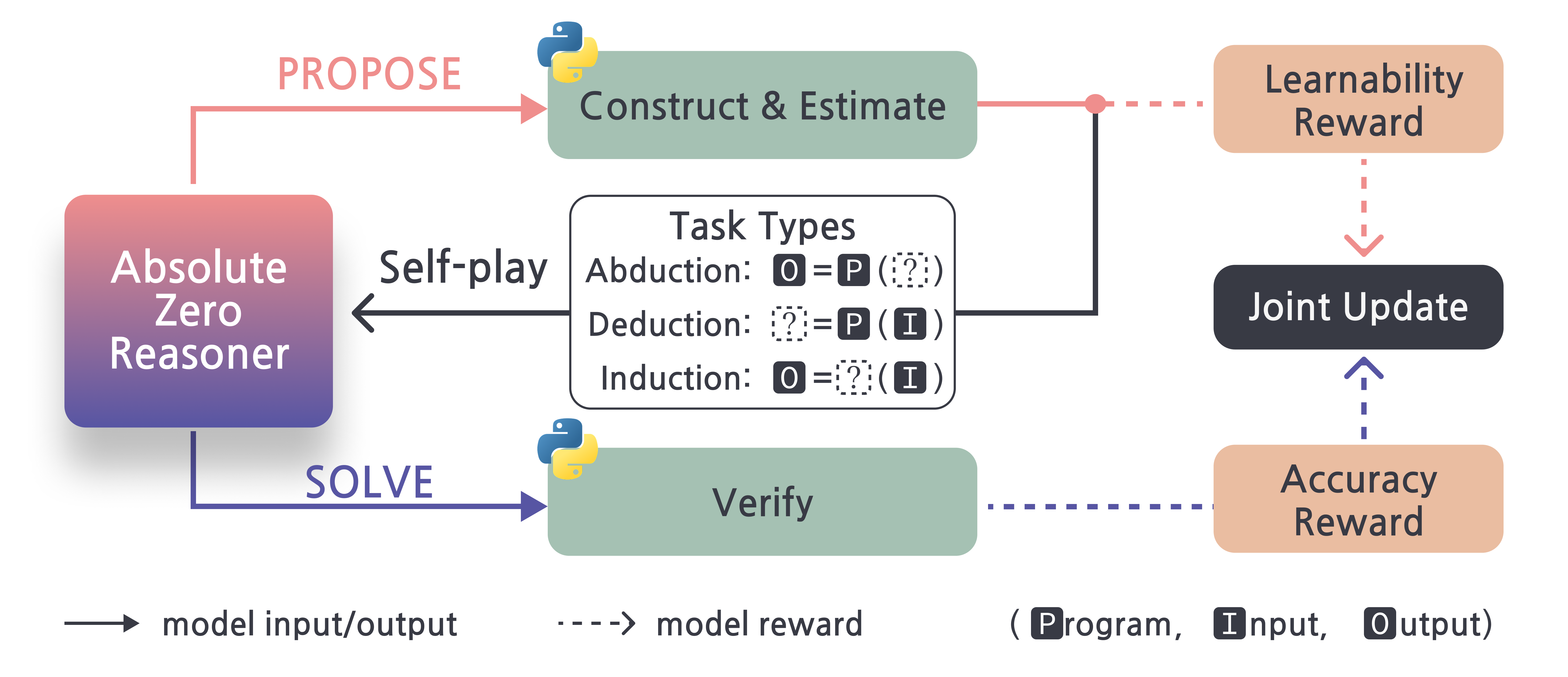
Absolute Zero Reasoner Training Overview. At every iteration, Absolute Zero Reasoner first PROPOSES a batch of tasks, conditioned on past self-generated triplets stored in a buffer and a particular task type: abduction, deduction, or induction. From these generated tasks, Python is used to filter and construct valid code-based reasoning questions. A learnability reward \(r_\text{propose}\) is also calculated for each proposed task. The Absolute Zero Reasoner then SOLVES the batch of reasoning questions. Python is used again to verify the generated responses and compute the accuracy reward \(r_\text{solve}\). Finally, the Absolute Zero Reasoner is jointly updated using both \(r_\text{propose}\) and \(r_\text{solve}\) across all three task types, using TRR++.

2.3. Absolute Zero Reasoner Algorithm

3. Results

3.1. Main Results

Model	Base	#data	HEval⁺	MBPP⁺	LCBv5	AME24	AME25	AMC	M500	Minva	Olypiad	CAvg	MAvg	AVG
Base Models
Qwen2.5-7B	-	-	73.2	65.3	17.5	6.7	3.3	37.5	64.8	25.0	27.7	52.0	27.5	39.8
Qwen2.5-7B-Ins	-	-	75.0	68.5	25.5	13.3	6.7	52.5	76.4	35.7	37.6	56.3	37.0	46.7
Qwen2.5-7B-Coder	-	-	80.5	69.3	19.9	6.7	3.3	40.0	54.0	17.3	21.9	56.6	23.9	40.2
Qwen2.5-7B-Math	-	-	61.0	57.9	16.2	10.0	16.7	42.5	64.2	15.4	28.0	45.0	29.5	37.3
Zero-Style Reasoners Trained on Curated Coding Data
AceCoder-RM	Ins	22k	79.9	71.4	23.6	20.0	6.7	50.0	76.4	34.6	36.7	58.3	37.4	47.9
AceCoder-Rule	Ins	22k	77.4	69.0	19.9	13.3	6.7	50.0	76.0	37.5	37.8	55.4	36.9	46.2
AceCoder-RM	Coder	22k	78.0	66.4	27.5	13.3	3.3	27.5	62.6	29.4	29.0	57.3	27.5	42.4
AceCoder-Rule	Coder	22k	80.5	70.4	29.0	6.7	6.7	40.0	62.8	27.6	27.4	60.0	28.5	44.3
CodeR1-LC2k	Ins	2k	81.7	71.7	28.1	13.3	10.0	45.0	75.0	33.5	36.7	60.5	35.6	48.0
CodeR1-12k	Ins	12k	81.1	73.5	29.3	13.3	3.3	37.5	74.0	35.7	36.9	61.3	33.5	47.4
Zero-Style Reasoners Trained on Curated Math Data
PRIME-Zero	Coder	484k	49.4	51.1	11.0	23.3	23.3	67.5	81.2	37.9	41.8	37.2	45.8	41.5
SimpleRL-Zoo	Base	8.5k	73.2	63.2	25.6	16.7	3.3	57.5	77.0	35.7	41.0	54.0	38.5	46.3
Oat-Zero	Math	8.5k	62.2	59.0	15.2	30.0	16.7	62.5	80.0	34.9	41.6	45.5	44.3	44.9
ORZ	Base	57k	80.5	64.3	22.0	13.3	16.7	60.0	81.8	32.7	45.0	55.6	41.6	48.6
Absolute Zero Training w/ No Curated Data (Ours)
AZR (Ours)	Base	0	71.3 -1.9	69.1 +3.8	25.3 +7.8	13.3 +6.6	13.3 +10.0	52.5 +15.0	74.4 +9.6	38.2 +13.2	38.5 +10.8	55.2 +3.2	38.4 +10.9	46.8 +7.0
AZR (Ours)	Coder	0	83.5 +3.0	69.6 +0.3	31.7 +11.8	20.0 +13.3	10.0 +6.7	57.5 +17.5	72.6 +22.6	36.4 +19.1	38.2 +16.3	61.6 +5.0	39.1 +15.2	50.4 +10.2

Performance of RL-Trained Reasoner on Reasoning Benchmarks Based on Qwen2.5-7B Models. Performance of various models is evaluated on three standard code benchmarks (HumanEval⁺, MBPP⁺, LCB v5) and six math benchmarks (AIME'24, AIME'25, AMC'23, MATH500, Minerva, OlympiadBench). Average performance across coding and math benchmarks is calculated as average of the two averages: AVG = (CAvg + MAvg) / 2. We use + for absolute percentage increase from base model. All models are trained using different variants of the Qwen2.5-7B model, with the variant and data usage labeled.

3.2. Scaling Results

Model Family	Variant	Code Avg	Math Avg	Total Avg
Qwen2.5-3B Coder		51.2	18.8	35.0
Qwen2.5-3B Coder	+ AZR (Ours)	54.9 +3.7	26.5 +7.7	40.7 +5.7

Qwen2.5-7B Coder		56.6	23.9	40.2
Qwen2.5-7B Coder	+ AZR (Ours)	61.6 +5.0	39.1 +15.2	50.4 +10.2

Qwen2.5-14B Coder		60.0	20.2	40.1
Qwen2.5-14B Coder	+ AZR (Ours)	63.6 +3.6	43.0 +22.8	53.3 +13.2

Out-of-distribution reasoning performance across different model sizes, reported as the average of code tasks, math tasks, and their overall average. We examine the effects of scaling model size from 3B to 14B parameters.

Given the strong performance of coder models in the 7B category, we extend the analysis by evaluating smaller and larger variants: Qwen2.5-3B-Coder and Qwen2.5-14B-Coder. Due to the absence of existing baselines for these zero-style reasoner models, we compare each model's performance to its corresponding base coder model.

The results reveal a clear trend: our method delivers greater gains on larger, more capable models. In the in-distribution setting, the 7B and 14B models continue to improve beyond 200 training steps, whereas the smaller 3B model appears to plateau. For out-of-distribution domains, larger models also show greater overall performance improvements than smaller ones: +5.7, +10.2, +13.2 overall performance gains, respectively for 3B, 7B and 14B. This is an encouraging sign, suggesting that scaling enhances the effectiveness of AZR. In future work, we aim to investigate the scaling laws that govern performance in the Absolute Zero paradigm.

3.3. Other Key Findings

Code priors amplify reasoning. The base Qwen-Coder-7b model started with math performance 3.6 points lower than Qwen-7b. But after AZR training for both models, the coder variant surpassed the base by 0.7 points, suggesting that strong coding capabilities may potentially amplify overall reasoning improvements after AZR training.
Cross domain transfer is more pronounced for AZR. After RLVR, expert code models raise math accuracy by only 0.65 points on average, whereas AZR-Base-7B and AZR-Coder-7B trained on self-proposed code reasoning tasks improve math average by 10.9 and 15.2, respectively, demonstrating much stronger generalized reasoning capability gains.
Comments as intermediate plans emerge naturally. When solving code induction tasks, AZR often interleaves step-by-step plans as comments and code (see Figure 4), resembling the ReAct prompting framework. Similar behavior has been observed in much larger formal-math models such as DeepSeek Prover v2 (671B). We therefore believe that allowing the model to use intermediate scratch-pads when generating long-form answers may be beneficial in other domains as well.
Cognitive Behaviors and Token length depends on reasoning mode. Distinct cognitive behaviors—such as step-by-step reasoning, enumeration, and trial-and-error all emerged through AZR training, but different behaviors are particularly evident across different types of tasks, a canonical example is trial-and-error in abduction, as shown in Figure 5. Furthermore token counts grow over AZR training, but the magnitude of increase also differs by task types: abduction grows the most because the model performs trial-and-error until output matches, whereas deduction and induction grow modestly.
Safety alarms ringing. We observe AZR with Llama3.1-8b as the base occasionally produces concerning chains of thought, we term the "uh-oh moment", example shown in Figure 6, highlighting the need for future work on safety-aware training.

Example of Comments as Intermediate Plans. The model naturally develops a habit of using comments as intermediate planning steps when solving complex reasoning tasks, similar to the ReAct prompting framework. This emergent behavior demonstrates how the model breaks down problems into manageable steps through self-commentary.

Example of a Model-Proposed Task and Its Response for Solving an Abduction Task. (Left) The model autonomously proposes an input and program for the abduction task. We execute the program to verify its validity and obtain the corresponding output. (Right) The model's reasoning process when solving the abduction task: given the code and output, it attempts to infer the original input. The model begins by analyzing the program, proposes an initial input, and reasons through the code to produce an output. If there is a mismatch, it reflects on the discrepancy and iteratively adjusts the input until the generated output matches the target. Interestingly, the agent arrives at a different input than the gold one, but since it produces the correct output, the answer is considered correct.

Safety Concerns in Reasoning — Example of "Uh-Oh Moment" in AZR Training. When using Llama3.1-8b as the base model, we occasionally observe concerning chains of thought during reasoning. This example highlights the need for safety-aware training in future iterations of the Absolute Zero paradigm.

4. Citation

@misc{zhao2025absolutezeroreinforcedselfplay,
    title={Absolute Zero: Reinforced Self-play Reasoning with Zero Data}, 
    author={Andrew Zhao and Yiran Wu and Yang Yue and Tong Wu and Quentin Xu and Yang Yue and Matthieu Lin and Shenzhi Wang and Qingyun Wu and Zilong Zheng and Gao Huang},
    year={2025},
    eprint={2505.03335},
    archivePrefix={arXiv},
    primaryClass={cs.LG},
    url={https://arxiv.org/abs/2505.03335}, 
}

Absolute Zero: Reinforced Self-play Reasoning with Zero Data

Abstract & Motivation

Out-of-Distribution General Reasoning Performance

AZR Proposed Programs

Spinning Hexagon Vibe Check

AZR-Coder-14b (Ours)

GPT-4o-mini

Qwen2.5-72B-Instruct

Qwen2.5-32B-Instruct

Qwen2.5-14B-Instruct

1. Absolute Zero Paradigm

2. Absolute Zero Reasoner

2.1. Propose and Solve Roles

2.2. Reasoning Modes

2.3. Absolute Zero Reasoner Algorithm

3. Results

3.1. Main Results

3.2. Scaling Results

3.3. Other Key Findings

4. Citation